一句话来概括两种方式的内容和区别就是:
等额本金:本金保持相同,利息逐月递减,月还款数递减;
等额本息:本金逐月递增,利息逐月递减,月还款数不变。
我们先来讲下等额本息和等额本金的概念。
等额本金就是每月还款的本金一样,即借款人每月按相等的金额(贷款金额/贷款月数)偿还贷款本金,每月贷款利息按月初剩余贷款本金计算并逐月结清,两者合计即为每月的还款额。
等额本息每月还款额一样,即每月本金与利息之和不变,但本金与利息比例是变化的。比方说等额本息每月还款1000元,第一月还款的1000元中本金是230,利息是770元;由于第一月还了230本金,利息相应减少,而每月还款额一样,所以本金比例增加。则第二月的1000元中本金是231,利息是769元。直至最后一月还款的1000元本金是996,利息是4元。
一区别
01
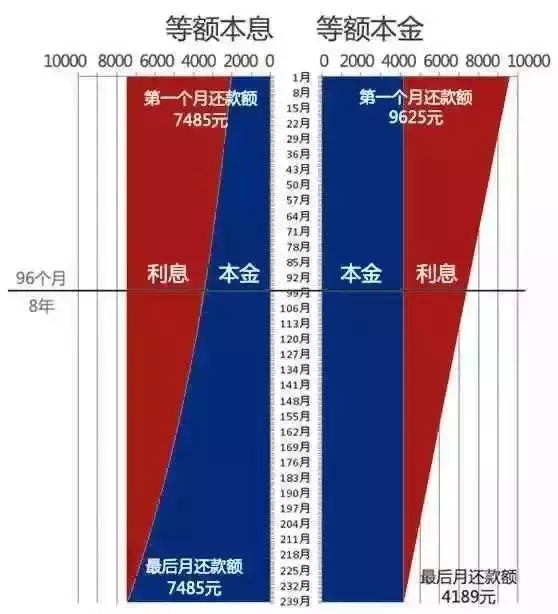
在贷款期限、金额和利率都相同的条件下,还款初期,等额本金还款方式每月归还的金额要大于等额本息。但按照还款总额计算,等额本金还款方式的还款总额更低。
02
有一定经济基础从而能承受前期较大还款压力适合等额本金还款方式,且提前要作出还款计划。经济条件不允许、收入处于较稳定状态的借款人适合等额本息还款方式,每月归还相同的款项,这样更方便安排收支。
还款计算公式
等额本金计算公式:
1.每月还款额=每月还款本金+每月还款利息;
2.每月还款本金=贷款总额/贷款月数 ;
3.每月还款利息=贷款本金余额*贷款月利率 (贷款月利率=年利率/12);
4.贷款本金余额=贷款总额-已还款月数*每月还款本金。
举个例子:
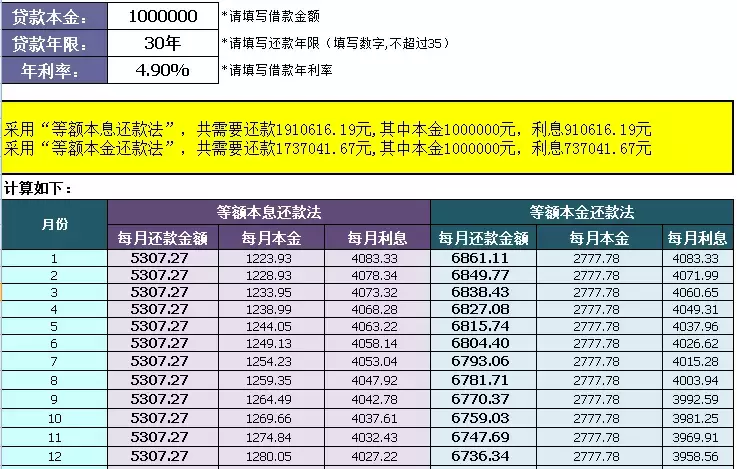
比如贷款100万;贷款30年;当前利率4.9%计算:
每月还款本金=1000000/360=2777.78元;
第一个月还利息=1000000*4.9%/12=4083.33元;
第一个月还款总额=2777.78+4083.33=6861.11元
第二个月还利息减少:2777.78*4.9%/12=11.34元
第二个月还款总额=6861.11-11.34=6849.77元;
以后每月递减11.34元。
总还款额为1737041.67元,其中利息为737041.67元
等额本息计算公式:
方法稍复杂,具体公式:
1.每月应还款额=借款本金×月利率×(1+月利率)^还款月数/[(1+月利率)^还款月数-1]
2.总还款额=每期还款额*还款月数。
举个同样的例子:贷款100万, 时间30年,利率按照当前利率4.9%计算:
每月应还款额=1000000×4.9%/12×(1+4.9%/12)^360/[(1+4.9%/12)^360-1]
=5307.267元
总还款额=5307.267*360= 1910616.12 元
二提前还款选择谁
等额本金前期还款中,本金多、利息少,更适合提前还款。
等额本息前期还款中,本金少,利息多,不适合提前还款。
三按照总额哪个划算
等额本息利息总额要比等额本金利息总额高接近14万元。所以,按照总额,等额本金还款更划算。
月供及利息对比
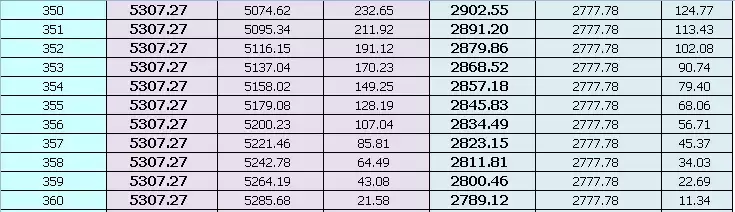
以下是两种还款方式的月供明细。
四等额本金的特征
每月的还款额不同,且逐月递减。它将贷款本金按还款的总月数均分,加上上期剩余本金的利息,形成月还款额,因此,等额本金第一个月还款额最多 ,然后逐月减少。
五等额本息的特征
每月的还款额相同。其中,本金所占比例逐月递增,利息所占比例逐月递减,所以,月还款数不变。前半段时期所还的每月金额中,利息比例大、本金比例小;还款期限过半后,转为本金比例大、利息比例小。
六等额本金利息的算法
等额本金贷款采用复合利率计算利息。每期还款结算时,剩余本金所产生的利息和剩余的本金(贷款余额)一起计息,换句话说就是,未付的利息也要计息。国外,放贷人更崇尚此种贷款方式。
上面提到由于通货膨胀及选择高投资收益,我们宁可多欠银行钱的方式来抵消通货膨胀的恶劣影响。
但是,有别于先息后本的最后一个月才还本金,不管等额本息还是等额本金,每个月都需要还掉部分本金。除了第一个月,我们用足贷款额度外,剩下的月份里,实际利用额度是逐月递减的。那么等额本金和等额本息具体的本金利用率有多少呢?
我们仍以贷款100万,年利率4.9%,借款30年,来比较下两者的差异。
等额本金法本金利用率
每个月还的本金是:1000000/360=2777.78元
我们引入衡量本金使用量:元*月,元*年。如1元用了1个月,就是1(元*月)。10000元用了1个月,就是10000(元*月)。1元用了1年,就是1元*年=12*1(元*月)
第一个月还的本金的使用量:1000000/360元*(1个月)=100000/360*1(元*月)(第一个月还的本金,实际上只用了1个月)
第二个月还的本金的使用量:1000000/360元*(2个月)=100000/360*2(元*月)(第二个月还的本金,实际上只用了2个月),以此类推。
第三个月还的本金的使用量:1000000/360元*(3个月)=100000/360*3(元*月)
……
第360个月还的本金的使用量:1000000/360元*(360个月)=100000/360*360(元*月)
那么,360个月一共的本金使用量
=1000000/360*(1+2+……+360)(元*月)
=1000000/360*(360*361/2)(元*月)
=1000000*361/2(元*月)
=1805000000(元*月)
=1805000000/12(元*年)
=150416667(元*年)
也就是说30年一共用了这个多本金,那么平均到每一年用的本金就是:150416667(元*年)/30年=501389元。
等额本息法本金利用率
等额本息的算法逻辑和上面是一样的,只不过等额本息还款法每个月还的本金不同,同样的逻辑能够得出答案:等额本息还款法下平均每年用的本金额=619467元。
所以, 等额本金法实际使用的本金是501389元,等额本息法实际使用的本金619467元。同样的贷款金额、期限、利率下,等额本息和等额本金两种方式实际使用的本金不同,等额本息实际使用的本金更多。
七等额本息利息的算法
等额本金贷款采用简单利率方式计算利息。每期还款结算时,对剩余的本金(贷款余额)计息,未支付的贷款利息不与未支付的贷款余额一起作利息计算,只有本金才作利息计算。
同理, 可以算出100万在1年、2年、3年、10年、20年、30年期下,两种不同还款方式实际使用的本金和支付的利息。
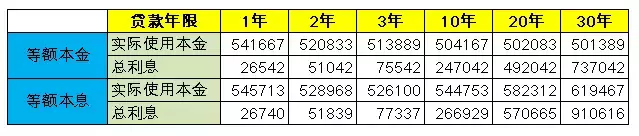
我们可以发现:等额本金的实际资金利用率均在50%上下浮动。等额本息的实际资金利用率随着贷款年限的增加,由54%逐步递增到62%。只可惜按揭贷款最长年限为30年,否则资金利用率还能进一步提高。
